常见的排序算法有：

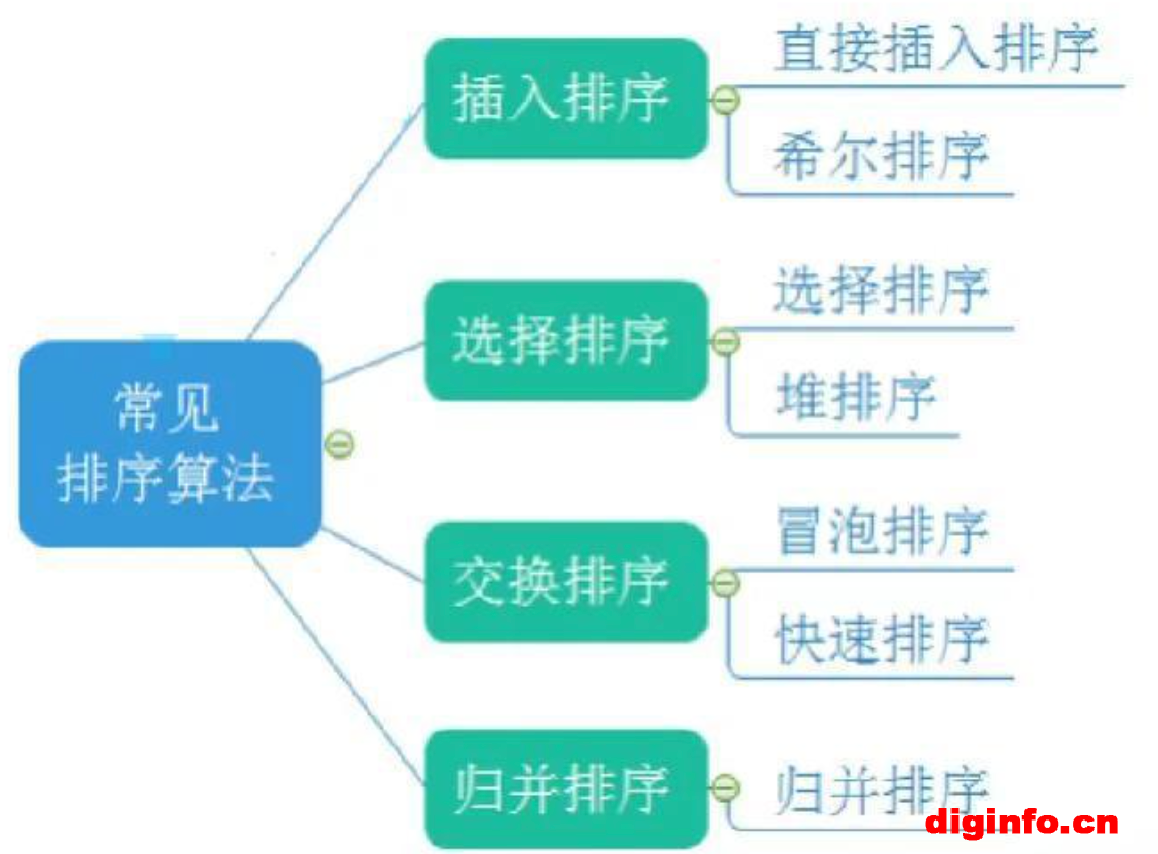
一.简单排序
1.1、冒泡排序:
冒泡排序是一种简单的排序算法，它的基本思想是比较相邻的元素并交换位置，从而将较大的元素“冒泡”到数列的末尾，而较小的元素则会沉到数列的开头。该算法的时间复杂度为O(n^2),不适合处理大规模的数据。
  public void  bubbleSort(int [] arrays){
       for (int i = arrays.length-1; i >0 ; i--) {
           for (int j = 0; j < i; j++) {
               int first = arrays[j];
               int two = arrays[j + 1];
               if(first>two){
                   arrays[j]=two;
                   arrays[j+1]=first;
               }
           }
       }
   }
1.2、选择排序:
选择排序是一种简单的排序算法，其基本思想是每次从未排序的数据中选择最小（或最大）的元素，放到已排序序列的末尾，直到全部排序完毕。该算法的时间复杂度为O(n^2)，不适合处理大规模的数据。

 public void selectSort(int [] arrays){
       for (int i = 0; i < arrays.length-1; i++) {
           int minIndex=i;
           int min = arrays[i];
           for (int j = i+1; j < arrays.length; j++) {
               int two = arrays[j];
               //正序
               if(min>two){
                   minIndex=j;
                   min=two;
               }
           }
           int temp=arrays[i];
           arrays[i]=min;
           arrays[minIndex]=temp;
       }
   }

1.3、插入排序:
插入排序是一种简单的排序算法，其基本思想是将待排序的数据分为已排序和未排序两个部分，初始时已排序部分只包含第一个元素，然后从未排序部分依次取出元素，插入到已排序部分的适当位置，直到全部排序完毕。该算法的时间复杂度为O(n^2)，不适合处理大规模的数据。

public void chaRu(int [] arrays) {
       for (int i = 1; i < arrays.length; i++) {
           for (int i1 = i; i1 >0; i1--) {
               int first = arrays[i1];
               int two = arrays[i1 - 1];
               if(first<two){
                   arrays[i1 - 1]=first;
                   arrays[i1]=two;
               }else {
                   break;
               }
           }
       }
   }

二.高级排序
2.1、希尔排序:
希尔排序是插入排序的一种改进版本，也称为“缩小增量排序”。它通过将待排序的序列划分成多个子序列来提高插入排序的效率，每个子序列的元素是互相间隔固定的，然后对每个子序列进行插入排序，最终合并成一个完整的有序序列。
希尔排序的时间复杂度取决于选择的增量序列，通常使用的增量序列是Shell提出的序列：n/2, n/4, …, 1。该算法的时间复杂度为O(n2)，但实际运行效率比其他O(n2)算法要高。
 public void xier(int[] a) {
       int n = a.length;
       int h = 1;
       //获取希尔排序得增量初始值
       while (h < n / 2) {
           h = h * 2 + 1;
       }
       xierSort(a, h, n);
}
public void xierSort(int[] a, int h, int len) {
       while (h > 0) {
           for (int i = h; i < len; i++) {
               int temp = a[i];
               int j = i;
               while (j >= h && a[j - h] > temp) {
                   a[j] = a[j - h];
                   j -= h;
               }
               a[j] = temp;
           }
           h = h / 2;
       }
   }
2.2、归并排序:
归并排序是一种基于分治思想的排序算法，其基本思想是将待排序的数组分成若干个子数组，然后将每个子数组排序，最后将已排序的子数组合并成一个完整的数组。时间复杂度为O(nlogn)
具体步骤如下：
1.分割：将待排序的数组按照二分法原则分成左右两个子数组，直到每个子数组只剩下一个元素为止。
2.合并：对于两个已经排好序的子数组，将它们合并成一个有序的数组。
3.重复：对于每个子数组，递归地执行步骤1和步骤2，直到所有的子数组都排好序为止。
 public void guiBing(int[] array) {
       guiBingSort(array, 0, array.length - 1);
}
   
public void guiBingSort(int[] array, int lo, int hi) {
       if (hi <= lo) {
           return;
       }
       int mid = (lo + hi) / 2;
       guiBingSort(array, lo, mid);
       guiBingSort(array, mid + 1, hi);
       guiBingMerge(array, lo, mid, hi);
}
 
private void guiBingMerge(int[] array, int lo, int mid, int hi) {
       //定义三个指针
       int left = lo, right = mid + 1, temp = 0;
       int[] tempArray = new int[hi - lo + 1];
       //合并数据左右数组
       while (left <= mid && right <= hi) {
           //拿出左边元素
           int leArray = array[left];
           //拿出右边元素
           int riArray = array[right];
           if (leArray < riArray) {
               tempArray[temp++] = array[left++];
           } else {
               tempArray[temp++] = array[right++];
           }
       }
       
       //如果右子数组没有数据 子数组又数据
       while (left <= mid) {
           tempArray[temp++] = array[left++];
       }
       //如果左子数组没有数据 右子数组又数据
       while (right <= hi) {
           tempArray[temp++] = array[right++];
       }
       //替换原数组数据
       int index = lo;
       int i = 0;
       while (index <= hi) {
           array[index++] = tempArray[i++];
       }
}  
2.3、快速排序:
快速排序（QuickSort）是一种基于比较的排序算法，它采用分治的思想，将一个大的问题分成两个小的问题，然后将这些小问题递归地解决。具体而言，快速排序的算法流程如下：
选择一个基准元素（pivot），通常选择数组的第一个元素或最后一个元素。
将数组中小于基准元素的数移到基准元素的左边，将大于基准元素的数移到基准元素的右边。
对基准元素左右两个子数组重复步骤1和步骤2，直到子数组的大小为1或0。
由于快速排序采用分治的思想，它的时间复杂度为O(nlogn)。在实际应用中，快速排序是一种高效的排序算法，尤其是对于大规模的数据集合。
 public void kuaiPai(int[] array) {
     kuaiPaiSort(array, 0, array.length - 1);
}

public void kuaiPaiSort(int[] array, int low, int hi) {
       if (low >= hi) {
           return;
       }
       int i = kauiPaiPartition(array, low, hi);
       //左边
       kuaiPaiSort(array, low, i - 1);
       //右边
       kuaiPaiSort(array, i + 1, hi);
   }

public void int kauiPaiPartition(int[] array, int low, int hi) {
       //最小得未分治分割点
       int key = array[low];
       int left = low + 1, height = hi;
       while (left < height) {
           if (array[left] < key) {
               left++;
           } else if (array[height] > key) {
               height--;
           } else {
               swap(array, left, height);
           }
       }
       swap(array, left, low);
       return left;
   }
   
public void swap(int[] array, int i, int j) {
       int temp = array[i];
       array[i] = array[j];
       array[j] = temp;
   }